Molecular Specification via a Simple Scripting Language

by
Peter C. McCluskey

Software consultant
Mountain View, CA 94040
pcm@rahul.net
http://www.rahul.net

This is a draft paper for a poster session at the
Sixth Foresight Conference on Molecular Nanotechnology

Abstract

Chemists have traditionally been mainly concerned with the study of natural molecules, which has led them to give little attention to the means of constructing descriptions of large artificial molecules. Nanotechnology designs will need ways to put together standard components to describe sophisticated systems.

This paper describes software under development that should make it easy to specify complex artificial molecules by simple scripts which describe moieties and how they attach to each other.

Each moiety description includes a list of dangling bonds plus a dihedral angle to specify the orientation of each dangling bond. The relative positions of the atoms in the moiety are specified by the bonds between them and as many dihedral angles as are needed to make it unambiguous.

The scripts are written in Python and use objects from Konrad Hinsen's Molecular Modelling Toolkit, which produces a powerful and flexible language without making the scripts hard to read or reinventing much syntax.

Motivations

When I set out to play with some molecular modelling software, I was disappointed to find that most of what I found was written around the "take what you see in nature and analyze it" approach, rather than an engineering approach to specifying molecules. This convinced me that if I wanted good software to enable me to create the kind of molecules I wanted to play with, I would need to write it myself.

Some people who think about nanotech design software focus on visual ways of specifying molecular systems. I doubt that a primarily graphical approach will scale up adequately. Small proteins or Drexler's example parts appear to be stretching the limits of what I can comprehend via a single picture. There are severe limits to how accurately I can position objects using a mouse when trying to control 6 degrees of freedom. GUI's impose important limitations on parallel operations that we might want to do on many disparate parts of a system.

The specific problem that provoked me into starting this software was the desire to find a good molecular equivalent to Lego (tm) Blocks.

I chose MMTK as the starting point for my efforts because it had the best combination of general purpose molecular modelling code, readability, and flexibility. Python's ability to import and parse code at runtime is an added bonus, which avoids the need to invent yet another scripting language.

The main drawback of Python is inadequate provision for type checking, which can lead to confusion and errors in passing objects to imperfectly documented parts of the system.

Unlike most software tools where there is a clear dividing line between the user interface and the internal implementation, the use of Python and MMTK provides a high-level interface designed specifically for most end users, but also allows sophisticated users access to most low-level methods in the system.

Users will need to learn some of the Python programming language, but it is unlikely that they will need to learn more than 5% of what it would take to become a serious Python programmer.

Overview of the Construction Process

The basic idea behind this software is that one should build up a modest library of simple moieties, and then describe how these moieties are bonded together or positioned relative to each other to form large systems.

Creating a Moiety

Create a file in the Groups subdirectory of your MMTK installation.
Start by creating the atoms using statements such as:
C1 = Atom('C')
(C1 is a name that will be used later to refer to this carbon atom later).
Then create bonds that connect the atoms using statements such as:
b12 = Bond(C1, C2)
This will sometimes be enough to specify the moiety shape, but more often you will need to constrain some of the dihedral angles (also known as torsion angles - which describe the angles between the plane of the first 3 of 4 atoms and the plane of the last 3 atoms) using statements such as:
da1 = Dihedral(C1, C2, C3, C4, 180*deg)
For moieties that are likely to be used with the Amber force field as it is currently implemented in MMTK, you will need to specify a mapping of atom names to Amber types such as:
amber_atom_type = {C1: 'CT', C2: 'CT', C3: 'CT', C4: 'CT' }
I have implemented an MM3 force field which can infer the correct atom types in many circumstances, and I hope that in the future the need for explicit atom type lists will become increasingly rare.

Next you need to list places where bonds can be attached to the moiety. The PrintDanglingBonds.py utility program will produce a list of statements such as:

dC3a = DanglingBond(C3, Dihedral(C1, C2, C3, None, -60.329439*deg))
which may be good enough, although it's probably a good idea to round the angles it produces to nicer numbers such as -60. The None in the Dihedral indicates where an atom from another moiety can be attached.

Finally, you should group the DanglingBond's into ordered sets with descriptive names to make it easier to specify how to attach other moieties:

hookwest = Hook(None, [dC1b, dC3a])
hooknorth = Hook(None, [dC1c])
(The None's in these examples don't serve any real purpose, and will probably become unneeded in a future version.

A simple example of a script to attach moieties together: 

block1 = Group('diamondoid_fragment')          # read in moiety
join = Joiner(block1)                          # create object that does joins
join.repeatGroup('hookeast', 'hookwest', 5)    # create 5 copies of block1
                                               # joined by hookeast, hookeast
result = join.getResult()                      # tell Joiner it's finished
result.setPositions(forcefield)                # assign coordinates to atoms
result.view()                                  # display results
To attach two different types of moieties together instead of repeating one type, you would use a joinGroups method call instead of repeatGroup:
join.joinGroups(block1.hookwest, moiety2.hook1)

Detailed Example

This example shows how my search for a molecular Lego (tm) block has been proceeding.

I start by creating the following straightish 4 carbon moiety: 

name = 'diamond4carbon'

C1 = Atom('C')
C2 = Atom('C')
C3 = Atom('C')
C4 = Atom('C')

b12 = Bond(C1,C2)
b23 = Bond(C2,C3)
b34 = Bond(C3,C4)

da1 = Dihedral(C1,C2,C3,C4,180*deg)

amber_atom_type = {C1: 'CT', C2: 'CT', C3: 'CT', C4: 'CT' }

dC1a = DanglingBond(C1, Dihedral(None,C1,C2,C3,60*deg))
dC1b = DanglingBond(C1, Dihedral(None,C1,C2,C3,-60*deg))
dC1c = DanglingBond(C1, Dihedral(C3,C2,C1,None,180*deg))
dC2a = DanglingBond(C2, Dihedral(None,C2,C3,C4,120*deg))
dC2b = DanglingBond(C2, Dihedral(None,C2,C3,C4,-120*deg))
dC3a = DanglingBond(C3, Dihedral(C1,C2,C3,None,60*deg))
dC3b = DanglingBond(C3, Dihedral(None,C3,C2,C1,120*deg))
dC4a = DanglingBond(C4, Dihedral(C2,C3,C4,None,60*deg))
dC4b = DanglingBond(C4, Dihedral(C2,C3,C4,None,-60*deg))
dC4c = DanglingBond(C4, Dihedral(C2,C3,C4,None,180*deg))

hooknorth = Hook(None, [dC1c])
hooksouth = Hook(None, [dC4c])
hookup   = Hook(None, [dC2b, dC4b])
hookdown = Hook(None, [dC1a, dC3b])
hookeast = Hook(None, [dC2a, dC4a])
hookwest = Hook(None, [dC1b, dC3a])
Most of the remaining code in this example comes from a script named lego6.py, and roughly corresponds to the chronological steps by which I proceeded.

Each excerpt is followed by some explanations. 

ff = GenericForceField('mm3')
world = InfiniteUniverse(ff)
block1 = Group('diamondoid_fragment')
join = Joiner(block1)
width = 5
join.repeatGroup('hookeast', 'hookwest', width)
join.repeatGroup('hooksouth', 'hooknorth', 5, 1, [180*Units.deg]*width)
join.repeatGroup('hookup', 'hookdown', 2)
result = join.getResult()
result.setPositions(ff)
The name result is now bound to a Group that is a roughly rectangular slab of 5 by (4*5)=20 by 2 carbons. The 1 in the middle repeatGroup call is an optional argument that controls whether the repeated block is reused or cloned. The list of width angles after it specifies the angles for the dihedrals about the single bond that connects each hooksouth Hook to each hooknorth. Ideally the software should be able to deduce that those are the only reasonable dihedral angles for those bonds, but it will take more programming effort to find a way of doing this that scales up well. The other hooks in this example all involve more than one bond, which automatically constrains the dihedral in a way that the software can deduce if the constraints are consistent with each other. 
a_hole = result.findAtomByName('diamond4carbon.diamond4carbon7.C4')
surface_point = Positioner.findNearestPointOnSurface(result, a_hole)
surface_vector = surface_point - a_hole.position()
dist_to_surface = surface_vector.length()
surface_dir = surface_vector.normal()
cylinder1 = Cylinder(a_hole.position() - 0.1*Units.Ang*surface_dir,\
		     2.5*Units.Ang, (1*Units.Ang+dist_to_surface)*surface_dir)
I want to dig a hole in one face of the slab. I looked at what the script had produced so far (using a version of RasMol that I have begun to integrate into MMTK), decided on an atom to center the hole around, and got it's name by clicking on it. I then created a line from that atom through the nearest point on the convex hull of the system (a set of triangles bounding the atom positions as closely as possible without making any concavities), and generated a cylinder about that line (extending the line a bit to make sure it included that atom and any other that might be on the cylinder boundary. 
atoms_in_cyl1 = result.atomsWithinRegion(cylinder1)
result.removeAtoms(atoms_in_cyl1, None)
This removes the atoms enclosed by the cylinder. 
c_below = result.findAtomByName('diamondoid_fragment.diamondoid_fragment32.C3')
nitrogen = result.generateNewAtom('N')
result.replaceAtoms([c_below], [nitrogen])
result.fillDanglingBonds(ff, 'N', 8, 3)
I saw that the carbon atom remaining at the center of the hole's bottom had a dangling bond remaining that might interfere with the way I hoped to insert things into the hole, so I replaced it with a nitrogen.

Six places where carbons had been removed left places to which 3 dangling bonds were pointing; the fillDanglingBonds call finds all such positions and fills them with atoms of symbol 'N', MM3 type 8. 

def filter2n(atom):                # define a function which returns true
    if atom.symbol != 'C':         # for carbons bonded to exactly 2 nitrogens
	return 0
    bonded_to = atom.bondedTo()
    countn = 0
    for a in bonded_to:
	if a.symbol == 'N':
	    countn = countn + 1
    return countn == 2

carbons_bonded_to_2_ns = filter(filter2n , result.atomList())
selected_ns = []
replace_cs = []
for a1 in carbons_bonded_to_2_ns:
    for a2 in a1.bondedTo():
	if a2.symbol == 'C':
	    c = a2
    a1_pos = a1.position()
    for a2 in a1.bondedTo():
	if a2.symbol == 'N':
	    x_product = (a1_pos - c.position()).cross(a2.position() - a1_pos)
	    if surface_dir * x_product > 0: # select by orientation
		selected_ns.append(a2)
    replace_cs.append(result.generateNewAtom('C'))
result.replaceAtoms(selected_ns, replace_cs, ff)
for i in range(len(carbons_bonded_to_2_ns)):        # make double bonds:
    result.attachBondBetween(carbons_bonded_to_2_ns[i], replace_cs[i])
I want to create some double bonds along the edge of the hole to make it moderately stable by itself, but still able (I hope) to react with similar double bonds on the knob I plan to insert into the hole.

First I search for all the carbon atoms attached to two nitrogens, which gives me three carbons associated with the six nitrogens I added in the prior step. I then identify three of the nitrogens on the basis of an arbitrarily chosen orientation from the selected carbons, replace those three nitrogens with carbons, and create double bonds from the previously selected carbons to the new carbons. The double bonds will be somewhat strained, but probably no more so than in figures 8.9 and 8.10 in NanoSystems (cubene and adamantene).

I'm now satisfied with the hole, and turn my attention to adding a knob on the other side of the slab that will fit into such a hole on another "Lego block". I create the following file cyanide: 

name = 'Cyanide'
C = Atom('C')
N = Atom('N')
b = Bond(C, N, 3)
mm3_atom_type = { C : 4, N : 10 }
db = DanglingBond(C, Dihedral(None, N, C, None, 0.0))
hook1 = Hook(None, [db])

Back to the main script: 

hook3_list = []
for db in result.danglingbonds:
    if nitrogen in db.a1.bondedTo():
	hook3_list.append(db)
hook3 = Hook((result, hook3_list))
join2 = Joiner(result)
layer = Group('lego4')
join2.joinGroups(hook3, layer.hook1, 0)
result = join2.getResult(0)
This creates a knob of three nearby cyanides. (Possibly the nitrogens will bond with neighboring cyanide carbons to form a ring. That would probably be equally close to the shape and reactivity I want). 
result.setPositions(ff)
result.hydrogenateDanglingBonds(ff)
This defines positions for the atoms in the knob, and adds fills all remaining dangling bonds with hydrogens. 
result2 = result.clone()
result2.name = 'd42'
face2 = []
for a in result2.atomList():
    if a.symbol == 'N':
	bonded = a.bondedTo()
	if len(bonded) == 1 and bonded[0].symbol == 'C':
	    face2.append(a)
face2 = [face2[0], face2[2], face2[1]]
PositionAdjacent(result,carbons_bonded_to_2_ns, result2,face2, [2*Units.Ang]*3)
Finally, I duplicate the molecule, pick three atoms on the knob of the new molecule, and rotate/translate it so those three atoms are 0.2 nanometers (2 angstroms) from three of the carbons on the edge of the original molecule's hole (actually, it can't satisfy those three constraints, and the actual distances are 0.2 to 0.32 nanometers (2 to 3.2 angstroms); see the PositionAdjacent description for details).

This produces a pair of molecules with potentially reactive double and triple bonds positioned 0.3 to 0.4 nanometers (3 to 4 angstroms) apart.


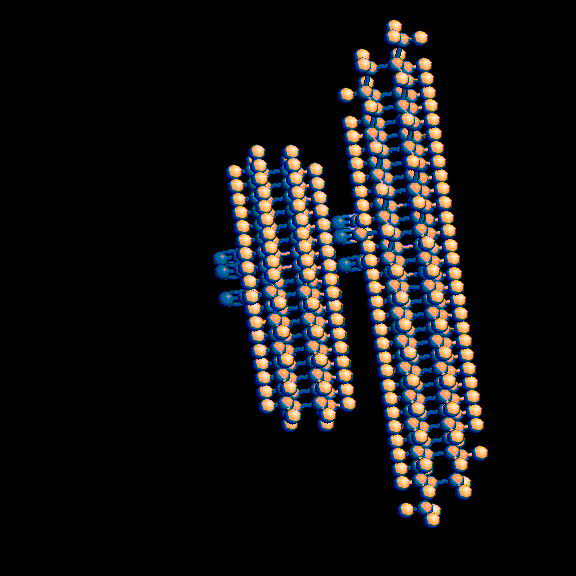
3-D representations of these images are available at http://www.rahul.net/pcm/mmtk/mnt6_images.html.

I plan to add another hole and another knob at the other end of the slab and run molecular dynamics simulations on the result to determine whether the three double bonds / triple bond pairs react to bond the two molecules together in a reasonably rigid result, and if so how closely they have to be positioned before they spontaneously form these bonds in a predictable one of the three possible orientations (each 120 degrees apart). If that works, I will tweak the shapes a bit so they fit well when I put many of them together into larger structures.

Prospects

If such building blocks could be created before a real assembler exists (a big assumption which I know I can't justify), then a positioning device with a fair amount of error might be able to construct a wide variety of atomically precise rigid structures.

I haven't yet addressed constructing systems which are capable of motion. I started with diamondoid systems because they are simpler to model, but I am equally interested in solution-based systems.

Will this approach work for floppy molecules such as DNA or proteins? I expect some problems associated with handling under-constrained dihedrals. I don't want to tackle the protein folding problem, but I also want to minimize the need for specifying dihedrals by users who are constructing systems from standardized components.

When I have the diamondoid tests sufficiently debugged, I will try designing some building blocks using DNA that have some hope of producing controlled motion and of being produced with today's technology.

Future Software Enhancements

Reference Manual

There is no well-defined line between what methods are intended for users writing scripts that construct systems, and methods that are intended for programmers implementing more methods, but this section will try to give specifications of those methods that are most useful for script writers.

Also, the toolkit is still in it's infancy as this paper is being written; this version is designed more to provide a taste of what the system can accomplish than as a programming guide.

Updated information will be available at http://www.rahul.net/pcm/mmtk/, along with more example scripts and pdb files they produce (such as "Hello, world!" written in hydroxyls on diamondoid), and source code.

Classes/Methods

Notations used:

References

 Lego is a trademark of the LEGO Group.

Corresponding Address:
Peter McCluskey
1571 El Camino Real W.,#15
Mountain View, CA 94040
(650) 967-3359
pcm@rahul.net
http://www.rahul.net/pcm



Foresight materials on the Web are ©1986-1998 Foresight Institute. All rights reserved.
Last updated 19Oct98. The URL of this document is not yet determined; see the following for more information about it:
http://www.rahul.net/pcm/mmtk/
http://www.foresight.org/Conferences/MNT6/
http://starship.skyport.net/crew/hinsen/mmtk.html